
不同于数组、队列等线性表的数据结构,树是一种非线性结构。除了树之外,图也是一种非线性结构。
二叉树如下所示。
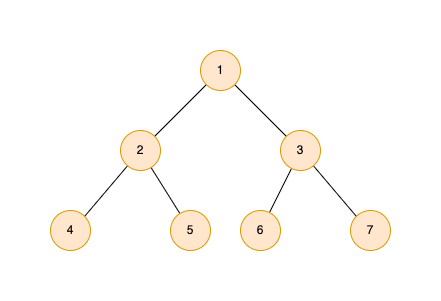
节点和边
在树中由节点和连接节点的边组成,二叉树最多有两个子节点。关于节点有几个概念:
- 父节点:节点 1 为节点 2 和 3 的父节点;
- 子节点:节点 4 和 5 为节点 2 的子节点;
- 兄弟节点:节点 2 和 3 为兄弟节点;
- 叶子节点:没有子节点的节点为叶子节点,如节点 4 和 5;
- 根节点:没有父节点的节点为根节点,如节点 1。
关于树的层级有如下几个概念:
- 节点的高度:该节点到叶子节点的最长路径,即边数;
- 节点的深度:根节点到该节点经历的边数;
- 节点的层数:深度 + 1;
- 树的高度:等于根节点的高度。
以下图为例,可以帮助理解节点高度、深度、层的概念。
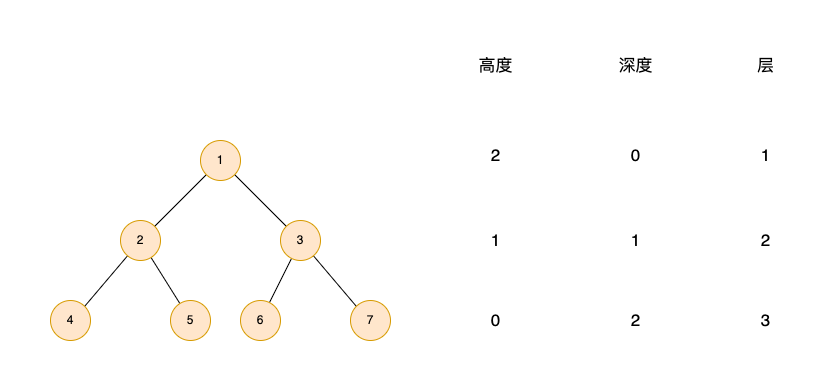
特殊的二叉树
如果一个二叉树叶子节点都在同一层级,而且除了叶子节点每个节点都有两个子节点,这种二叉树叫做满二叉树。上文中的图例即为满二叉树。
如果一个二叉树,最后一层的叶子节点都在左侧,其他层的节点数量达到最大,这种二叉树叫做完全二叉树。上文图中我们把节点 7 去掉,就符合满二叉树的条件。
二叉树的存储
二叉树的存储也离不开最基础的数据结构:
- 数组
- 链表
对于数组存储,我们可以使用以下规则约定每个节点在数组中存储的位置。
- 假设父节点存储索引为 i;
- 该节点左子节点的位置为 2 i,右子节点为 2 i + 1;
- 根节点存储在 1 号位。
下图可以帮助理解二叉树数组存储的方式。可以看到,完全二叉树使用数组存储能够充分利用数组空间。非完全二叉树则会导致数组空间的浪费。
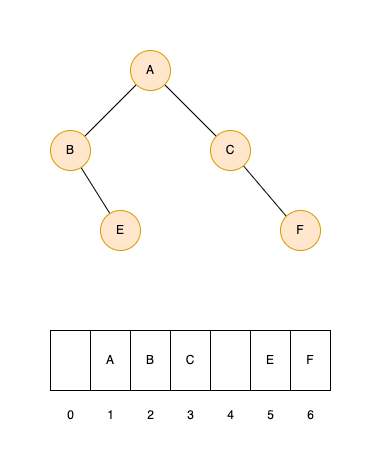
对于链表存储,我们使用如下结构进行构建二叉树。
class Node {
Node leftChild;
Node rightChild;
}
二叉树的遍历
树和图的遍历分为两种:
- 深度优先遍历:如果存在层级更深的子节点,优先遍历该节点,否则遍历同层级的其他节点;
- 广度优先遍历:如果存在同层级的兄弟节点,优先遍历兄弟节点,否则遍历子节点。
对于树的深度优先遍历,又分为三种:
- 前序遍历:访问当前节点——访问左子树——访问右子树;
- 中序遍历:访问左子树——访问当前节点——访问右子树;
- 后序遍历:访问左子树——访问右子树——访问当前节点。
仍以下图为例,其遍历序列分别如下:
- 前序遍历:1, 2, 4, 5, 3, 6, 7;
- 中序遍历:4, 2, 5, 1, 6, 3, 7;
- 后序遍历:4, 5, 2, 6, 7, 3, 1。

三种遍历的递归代码如下。
void preOrder(Node root) {
if (root == null) return;
print(root)
preOrder(root.left);
preOrder(root.right);
}
void inOrder(Node root) {
if (root == null) return;
inOrder(root.left);
print(root)
inOrder(root.right);
}
void postOrder(Node root) {
if (root == null) return;
postOrder(root.left);
postOrder(root.right);
print(root)
}
总结
本次我们了解了二叉树的基础知识,有二叉树的特征、二叉树的数组和链表存储方式、二叉树的遍历。有时间我们聊聊二叉树的应用,它是如何优化搜索算法复杂度的。